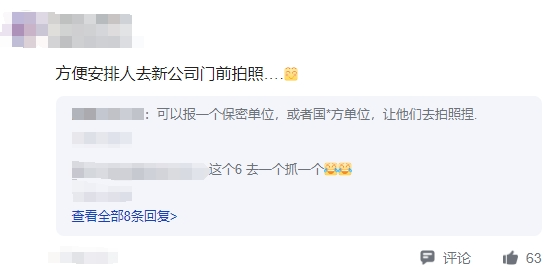
一般你从一个公司离职后，不说老死不相往来，也该是日渐疏远。但是一网友在网上发帖称，离职后，前公司竟然调查他们的去向。哦？难道是追夫火葬场？还是秘密监控？又或者是竞业协议？来看看网友们怎么看吧。 
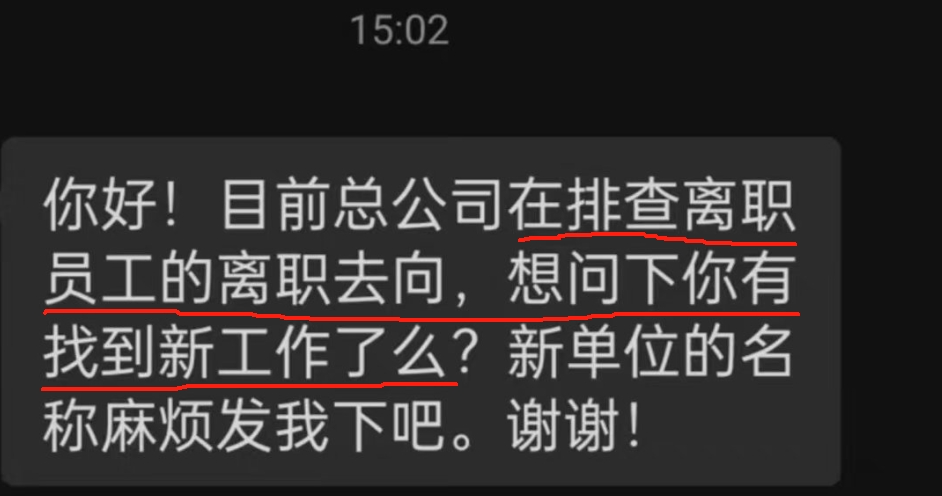
一网友也不惯着：“考公了，当地税务局”哈哈，从此翻身把歌唱。 
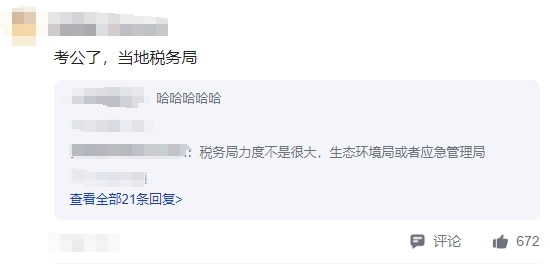
秀儿不止一个：“你就说在殡仪馆上班，负责烧人，问他需要合作不，量大从优”好家伙，谁敢和你合作，从此避你远远的。 
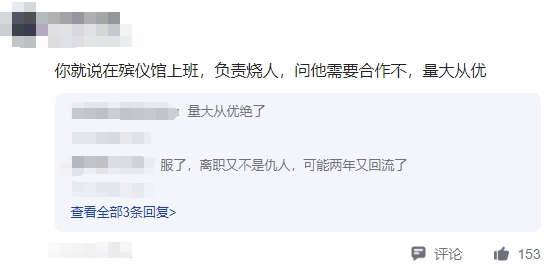
还有网友猜测：“方便安排人去新公司门前拍照。”电视剧都不这么演吧。 
更有秀儿直接：“已读不回”好好好，两极反转了是吧。 
看了一圈，感觉应该是竞业协议。什么是竞业协议，简单来说就是你签了这个后，在职或离职后一段时期内，不能从事于与原公司存在竞争的公司的行为。 
这个协议总感觉有点儿离谱啊，离职后还要看你的去向。那么大家怎么看呢？ 现在环境就这样，不管是大厂还是小厂的笔面试题都会考察算法，所以算法是你内卷路上不可或缺的模块。下面是今日算法题，来自LeetCode的第48题：旋转图像，下面是我的算法思路及实现，让我们来看看吧。 算法题目 给定一个 n x n 的二维矩阵，代表一个图像，请将图像顺时针旋转 90 度。 说明： 你必须在原矩阵上操作，不要使用另一个矩阵来旋转图像。 资源分享
算法思路 旋转图像可以通过以下步骤完成： 转置矩阵：即行变列，列变行。 反转每一行：将每一行的元素顺序翻转。
这样可以实现矩阵的顺时针旋转。 func rotate(matrix [][]int) { n := len(matrix)
// Transpose the matrix for i := 0; i < n; i++ { for j := i; j < n; j++ { matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j] } }
// Reverse each row for i := 0; i < n; i++ { for j, k := 0, n-1; j < k; j, k = j+1, k-1 { matrix[i][j], matrix[i][k] = matrix[i][k], matrix[i][j] } }}
Java实现public void rotate(int[][] matrix) { int n = matrix.length; // Transpose the matrix for (int i = 0; i < n; i++) { for (int j = i; j < n; j++) { int temp = matrix[i][j]; matrix[i][j] = matrix[j][i]; matrix[j][i] = temp; } } // Reverse each row for (int i = 0; i < n; i++) { for (int j = 0; j < n / 2; j++) { int temp = matrix[i][j]; matrix[i][j] = matrix[i][n - 1 - j]; matrix[i][n - 1 - j] = temp; } }}
JavaScript实现function rotate(matrix) { let n = matrix.length; // Transpose the matrix for (let i = 0; i < n; i++) { for (let j = i; j < n; j++) { let temp = matrix[i][j]; matrix[i][j] = matrix[j][i]; matrix[j][i] = temp; } } // Reverse each row for (let i = 0; i < n; i++) { matrix[i].reverse(); }}
Python 代码实现def rotate(matrix): n = len(matrix) # Transpose the matrixfor i in range(n): for j in range(i, n): matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
# Reverse each rowfor row in matrix: row.reverse()
算法解析转置矩阵：通过交换矩阵的行和列索引，我们可以实现矩阵的转置。在 i 从 0 到 n-1 循环中，j 从 i 到 n-1 的循环确保我们只交换上三角形部分，避免重复交换。 反转每行：每一行翻转是通过交换行内的首尾元素逐渐向中间靠拢实现的。这一步是完成旋转的关键，因为转置后的矩阵顺序还不符合顺时针旋转的要求。
以 3x3 矩阵为例，进行旋转操作： [ [1, 2, 3], [4, 5, 6], [7, 8, 9]]
[ [7, 4, 1], [8, 5, 2], [9, 6, 3]]
矩阵旋转是一个可以通过简单的数学操作实现的图像处理技巧。本文介绍的方法利用矩阵的转置和行反转来达到旋转的效果，不需要额外的存储空间，操作简单而高效。
| 
